Table of Contents
Koordinatsystem och gradnät
(Koordinatsystem,koordinat,gradnät,koordinater)
Introduktion till koordinatsystem
Koordinater utan något enhetligt system
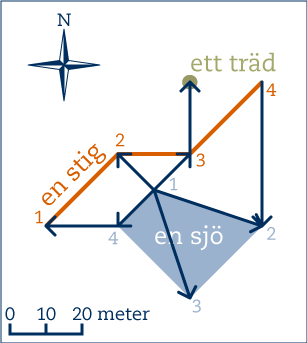
I vardagliga situationer beskrivs en position ofta i relation till andra platser. Antingen genom att beskriva avståndet (exempelvis att jag bor 'några hundra meter' från universitet) eller genom att ange riktningen relativt den plats man relaterar till (exempelvis jag bor 'söder om' Söder). Kombinationen av att ange avstånd och riktning från en utgångspunkt är egentligen en tillräcklig och fullständig beskrivning på platsers relativa förhållande till varandra. Tabellen nedan är exempelvis tillräcklig för att kunna rita upp kartan nedanför tabellen. De blå pilarna pekar ut de relativa beskrivningarna som nämns i tabellen.
| Position | Längd | Riktning | Utgångspunkt |
|---|---|---|---|
| trädets position | 20 m | norr om | stigens 3:e position |
| stigens 3:e position | 14 m | nordost om | sjöns 1:a position |
| stigens 2:a position | 14 m | nordväst om | sjöns 1:a position |
| sjöns 4:e position | 14 m | sydväst om | sjöns 1:a position |
| sjöns 2:a position | 32 m | ost sydost om | sjöns 1:a position |
| sjöns 3:e position | 32 m | syd sydost om | sjöns 1:a position |
| stigens 1:a position | 20 m | väster om | sjöns 4:e position |
| sjöns 2:a position | 40 m | söder om | stigens 3:e position |
Radiellt koordinatsystem
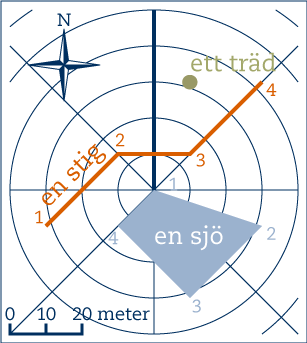
I det ovanstående exemplet finns det inget enhetligt sätt att ange en punkt. Ett ofta mer rationellt sätt att ange positionerna är att införa ett koordinatsystem. Exempelvis kan vi se att många av beskrivningarna ovan utgick i från sjöns 1:a position, så varför kan vi inte se till att alla punkter relateras till just den punkten. På det sättet slipper vi ange vilken punkt vi utgår ifrån för varje positionsangivelse, utan det är underförstått om vi anger att alla koordinater beskrivs utifrån det lokala koordinatsystemet LRKSJ1 (lokalt radiellt koordinatsystem från sjöns 1:a position).
Radiellt betyder helt enkelt att vi anger positioner med hjälp av avstånd och riktning från en mittpunkt.
| Position | Avstånd i meter | Riktning i grader (ett varv är 360 grader och norr = 0) |
|---|---|---|
| trädets position | 32 | 18 |
| stigens 1:a position | 32 | 252 |
| stigens 2:a position | 14 | 315 |
| stigens 3:e position | 14 | 45 |
| stigens 4:e position | 42 | 45 |
| sjöns 1:a position | 0 | 315 |
| sjöns 2:a position | 32 | 108 |
| sjöns 3:e position | 32 | 162 |
| sjöns 4:e position | 14 | 225 |
Kartesiskt koordinatsystem
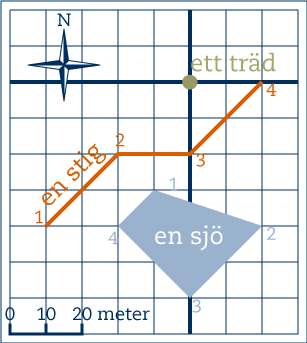
Ett annat sätt att definiera ett koordinatsystem är att ange exempelvis hur långt norr respektive hur långt öster om trädet de olika positionerna är (sjöns andra punkt ligger exempelvis 40 meter söder om trädet och 20 meter öster om det och får därför koordinaterna 40 och 20). Ett sådant koordinatsystem där avståndsrikningarna som mäts (i detta fall norr och öster) är vinkelräta mot varandra kallas kartesiskt. Här nedan visas en tabell där punkterna har angetts med ett kartesiskt koordinatsystem med trädet som origo (centralpunkt).
| Position | x koordinat | y koordinat |
|---|---|---|
| trädets position | 0 | 0 |
| stigens 1:a position | 40 | 40 |
| stigens 2:a position | 20 | 20 |
| stigens 3:e position | 20 | 0 |
| stigens 4:e position | 0 | 20 |
| sjöns 1:a position | 30 | 10 |
| sjöns 2:a position | 40 | 20 |
| sjöns 3:e position | 60 | 0 |
| sjöns 4:e position | 40 | 20 |
Observera att bokstäverna x och y i geografiska koordinatsystem används omvänt mot hur de vanligtvis används inom geometri. Här är alltså x uppåt (norrut) och y till vänster (österut) medan man inom geometri och matematik i allmänhet ofta har x åt höger och y uppåt.
Globala koordinatsystem
Radiella och kartesiska koordinatsystem förutsätter att jorden är platt (eller i varje fall konisk eller cylindrisk), något man kan räkna med att jorden är utan att det blir så väldigt fel om man använder koordinatsystemet över ett litet eller långsmalt område. Dessvärre är jordens form varken platt, konisk eller cylindrisk utan rund (eller egentligen inte det utan vid polerna tillplattad och allmänt bucklig, läs mer på Lantmäteriets hemsida om geoiden).
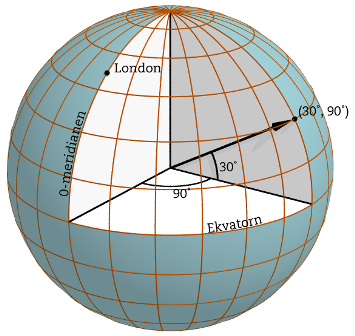
Så om vi skall använda koordinatsystemet över ett större område och vi tänker oss att jorden är rund kan vi införa ett 'gradnät 'som består av longituder (går från nordpol till sydpol) och latituder (går runt jorden på konstant avstånd från polerna, Ekvatorn är den längsta av latituderna). Figuren nedan visar ett sådant gradnät.
Olika koordinatsystem som brukar användas
Longitud och Latitud används relativt ofta då den geografiska informationen är för hela världen. WGS84 är ett vanligt koordinatsystem för hela jorden och är anpassad efter att jorden är lite tillplattad vid polerna.
För lokala förhållanden brukar man dock införa regionala eller nationella koordinatsystem. Under 2007 bytte Sverige koordinatsystem från det tidigare rikets nät (RT90 2,5 gon V) till Sweref 99. Så för all data som laddas ned från exempelvis GSD så gäller SWEREF 99. Var dock uppmärksam på att vissa andra datakällor kan leverera data i RT90 2,5 gon V.
På Lantmäteriets sidor om geodesi går det att läsa mer om olika koordinatsystem samt om närliggande ämnen.
Tips om hanterandet av projektioner och koordinatsystem i olika programvaror: